人工神经网络和反向传播算法
最近因为人机大战, 人工智能火得不行, 作为技术人员, 自然对这种终极技术产生了一定的兴趣, 翻了一些论文看了一些文档以后, 在这里记录一点学习心得吧.
人工智能原理
人工智能, 这个标题好像很厉害的样子, 实际上原理很简单, 就是一个强大的神经网络. 而神经网络又好像很厉害的样子, 下面就来看看神经网络是什么东西.
神经网络
基本概念
在深度学习中的神经网络, 和人体的神经网络一点关系都没有, 只是一个相似的名词而已. 这里的神经网络是由很多个神经节点构成, 可能有多层, 每层有n个, 就像n维数组一样, 每个神经节点都是一个多参数函数, 返回值是和下一层网络节点数量相同的sigmoid函数值. 同一层的每个节点的输出值经过求权和相加以后, 作为下一层的参数以供计算. 这便是神经网络最基本的实现方式.
原理
在宇宙中, 大概除了量子存在海森堡测不准原理以外, 其他的都是可测量和计算的. 如万有引力, 牛顿定律, E=mc^2等. 这种是简单的原理, 上升到复杂一点的, 如火箭升空, 需要多大的推动力, 能带多少燃料和多少负载, 能飞到什么地方和什么时候到, 都是可以计算出来的, 只是需要的条件和参数比较多. 以此类推到更复杂的情况, 可以得到, 任何事情或者说是变化都是可以计算出来的, 只是需要你传入准确的参数. 而在以前, 这些计算方法都是由人类创造和推出, 而在神经网络中, 是由算法和数据生成.
如以前的天气预报, 是通过各种风力风向温度湿度等, 传入一个复杂计算函数中得到结果, 往往会出现不准确的情况, 因为计算函数不完善, 而这种计算函数又是很难构建完善的. 而现在出现了人工智能加大数据分析预测天气情况, 比以前准确了许多, 而且会一直进化和提升.
假设以前的计算方法为, 指定一个函数f(x1,x2,x3...) = ax1 + bx2 + cx3 + ..., 传入足够的值来得到结果, 那么里面的参数列表a,b,c等值是通过历史数据计算得来. 计算参数起来就会特别复杂和麻烦, 而且并不能动态生成这个函数, 而神经网络则是类似这样, 不过是生成一个动态的参数表格.
先来看看单个的神经元, 为了方便计算和得出结果, 需要使神经元的输入值都为(0,1), 输出值也为(0,1), 这样在计算结果时, 接近1的为真, 接近0的为假. 为了将任意值都转换为(0,1)的形式, 需要定义一个sigmoid函数, sigmoid(z) = 1 / (1 + e^-z). 当输入值为很大的正数时, 那么e^-z值为很小, 函数返回值接近1, 当输入值为很大的负数时, e^-z变大, 函数返回值接近0, 而在中间值变化时, 该函数返回值也是平滑的, 所以可以比较好的模拟(0,1)的返回值. 不过如果你需要, 也可以实现一个其他的sigmoid函数, 只要返回值为平滑的(0,1)即可. 在看传入sigmoid函数的参数, 应该是传入值和该神经元初步计算得到的值. 表示为f(x1,x2...) = a1x1 + a2x2 + ... + b. 所以确定一个神经元, 只需要确定它的a1-an的值, 和偏移量b即可.
然后来看一个最简单的单层神经网络, 有一个输入层, 一个处理层, 一个输出层. 输入层输入值为{x1,x2,x3,x4}, 处理层有3个神经元, 那么它们的处理函数应该是f[a1](x1,x2,x3,x4) = sigmoid(a1a1 * x1 + a1a2 * x2 + a1a3 * x3 + a1a4 * x4 + a1b), f[a2](x1,x2,x3,x4) = sigmoid(a2a1 * x1 + a2a2 * x2 + a2a3 * x3 + a2a4 * x4 + a2b), f[a3](x1,x2,x3,x4) = sigmoid(a3a1 * x1 + a3a2 * x2 + a3a3 * x3 + a3a4 * x4 + a3b), 输出层只有一个神经元, 处理函数f[b1](xa1,xa2,xa3) = sigmoid(b1a1 * xa1 + b1a2 * xa2 + b1a3 * xa3 + b1b).
假设上面的神经网络是对真实情况的反应, 设y(x)为真实输出, f(x)为神经网络的输出. 在给定x的情况下, 需要找到合适的参数, 使f(x)值尽量等于y(x)的值. 那么问题就变成: 需要一个算法, 找到所有的参数an和bnb, 是输出值尽量靠近真实值. 为了知道如何才算靠近真实值, 需要定义一个代价函数: C(w,b) = E(x)(||y(x) - a||^2) / 2n, 这里面的a即为f(x)计算得到的值, E(x)(...)即为对所有的x值求和, 反映到实际即对于所有训练数据x, n为训练数据数量, 得到一个整体训练数据的误差, w为所有an的向量, b代表偏移. 而训练神经网络的目标, 便是让C(w,b)变得尽可能小.
现在, 将输入值x向量化看待, 每层的输入值为xn = {xn1,xn2,xn3,xn4}, 每层的计算函数为wn = {{a1a1,a1a2,a1a3,a1a4},{a2a1,a2a2,a2a3,a2a4},{a3a1,a3a2,a3a3,a3a4}}, 偏移量为bn = {b1b,b2b,b3b}, 那么在计算输出值的时候, 使用向量计算, 即可得到输出值f(x) = sigmoid(wn * xn + bn), 那么计算该层的输出值即为f(xi) = sigmoid(wn * x[i-1] + bn), 令z[i] = wn * x[i-1] + bn, 那么f(xi) = sigmoid(z[i]), 令z[i][j]为第[i]层的第[j]个值, 那么z[a][1]为第a层第1个值, 即为f[a1](x1,x2,x3,x4)所计算的值, 即z[a][1] = a1a1 * x1 + a1a2 * x2 + a1a3 * x3 + a1a4 * x4 + a1b, 那么z[i][j] = E(k)(a[i]a[j][k] * x[k]) + b[i][j].
下面来看看反向传播算法的含义吧. 假设在训练好的神经网络中, 每个神经元都有正确的参数, 而第i层第j个神经元被人为改变成了错误的参数. 那么在输入x的值时, 在计算结果经过这个神经元的时候, 值与原来的正确值有一点改变, 设改变值为Δz[i][j], 这就导致了神经元输出变成了f[i][j](x) = sigmoid(z[i][j] + Δz[i][j]). 这个改变将会在后续的网络中传播, 导致全部代价改变. 因为原始的代价函数为C = (y - a)^2 / 2, a = E(i,j)(z[i][j]), 那么代价改变值可以表示为ΔC = C′ * Δz[i][j], 那么C′ = d(C) / d(z[i][j]). 可以看出, 如果改变Δz[i][j], 便可以使C变化, 如果正确的改变Δz[i][j], 可以使得C值变小.
设第i层第j个神经元的错误量为δij = d(c) / d(z[i][j]), 那么它对i+1层的第 n 个神经元影响为a[i + 1][n] * δij.
在训练神经网络中, 参数计算是靠梯度批量下降法来寻找合适参数的, 那么便需要求误差函数对每个权重a和偏移b的偏导数. 如果是正常求值, 那么需要从输入节点开始, 将每个节点对下个节点的影响导数求出, 一直求到对最终结果的影响. 然后再根据最终结果对每个节点的偏导值, 来调整它们的权重和偏导数. 而反向传播算法则是改进这个计算方法的算法. 反向传播从最后一层节点开始计算它之前的每个节点对它的影响, 然后再依次前推, 那么一次性就能计算出所有的节点对最后一个节点的偏导值, 极大的简化了求值速度.
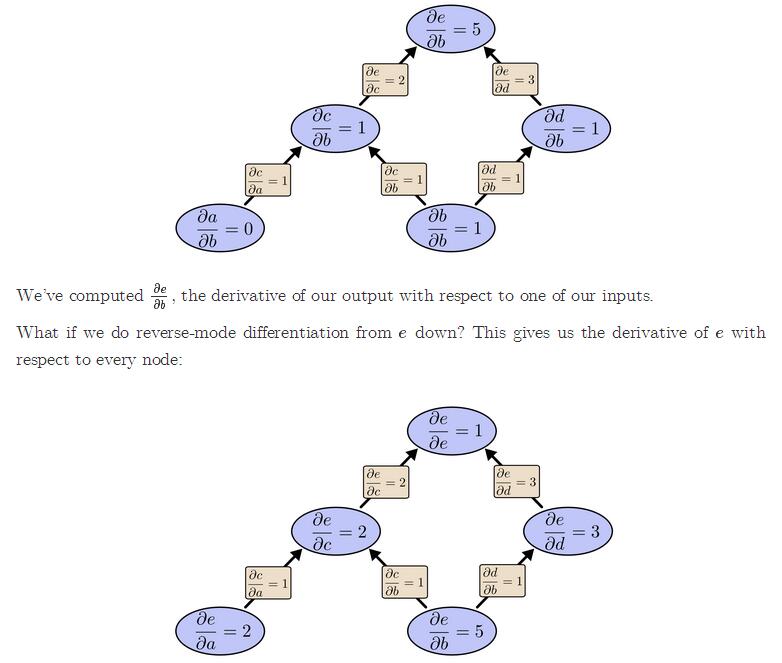
这便是反向传播的核心思想, 即快速计算出最终结果对每个节点参数的偏导值, 然后再根据梯度下降算法来更新每个节点的参数, 从而降低C的值, 进化神经网络. 而具体如何实现, 又是一个比较大的内容了, 可以参考这篇文章, 使用python实现一个简单的神经网络来识别图片.

